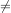 for inequality
for inequality
Copyright Notice
All materials in this document are copyrighted. The author reserves all rights. Infringements will be prosecuted at the maximum extent allowed by law.
You are permitted to do the following:
Don’t tell me because of the prerequisite, degree requirement or certificate requirement. You are taking this class because you are passionate about learning how to program a computer! You are taking this class because you think you will enjoy a career in computer programming!
In my honest and humble (as usual) opinion, it is so important that you feel passionate about computer programming to take on a computer programming course, or to choose a career in computer programming. In fact, as much as programming is about logic, your success in this course, subsequent programming courses and a programming career is about your passion in computer programming.
Okay, Tak, you have made your point. But why?
Unlike tasks involving mundane chore, programming requires a logical and analytical mind that keeps its cool when everything is falling apart. As a programmer, there will be days when you have a deadline that is yesterday, last week or last month! There will be days that you keep programming for more than 36 hours without sleeping. There are only a few things to keep you going:
An “algorithm” is a fancy word for instructions to solve a particular problem. As you see, the title of this class is rather redundant.
Some algorithms are easy to express. For example, the following algorithm washes dishes:
As you can see, most activities that we do everyday can be described by algorithms. This is hardly surprising because we are, for the most part, logical.
What is different about computer program algorithms is that such algorithms are very specific, and they specify details down to numerical and logical expressions. We will introduce these concepts in subsequent chapters.
I generally do not use the textbook. While you are more than welcome to keep your textbook, some of you may do just fine without one.
I post most of the course materials online. You can access such information at the home page for this class: http://www.drtak.org/teaches/ARC/cisp300. Please note that everything on my website is work-in-progress. This means everything is subject to change. Unless you have to, I suggest you view the materials online rather than printing them out.
As mentioned in an earlier section, you should sign up for a ZIP account to receive information regarding this class. This is the only way for you to receive your midterm and final grades. I will also send emails to your ZIP accounts regarding course materials and homework assignments. To sign up, visit http://zip.arc.losrios.edu on campus. Once you have signed up an account, you can access it via the internet (from any computer connected to the internet).
Just so that I know you know how to use ZIP mail, this is your homework assignment.
Pseudocode code has certain words borrowed from English and a funny way to indent sentences. This chapter introduces pseudocode and explains how to use constructs in pseudocode.
A simple statement in pseudocode is a step in the solution of a problem. For example, “locate a dirty dish” is one of the steps of washing dishes.
It is important to understand that statements in pseudocode are sequential. In other words, an agent performs statements on a step-by-step basis. The order of statement execution is top-to-bottom, much like the order of reading in most western languages.
Unlike most natural written languages, we only specify one and only one action in each statement. If you have two actions to perform, separate them to two statements. This makes the pseudocode representation of instructions a little lengthier than the natural language version.
Last but not least, statements of the same “level” have the same indentation from the left margin. At this point, this rule doesn’t seem to make much sense or be important. We will see later why this is such an important rule.
With simple statements, you can express algorithms that involve sequences. This is great, but instructions that involve only sequences are hardly interesting.
Let us consider the logic of shopping. What goes through your mind when you are looking at an item? In our example, let us consider a can of soda. For us programmers, soda is the sole source of energy and life-sustaining water.
I don’t know about you, but the first thing I consider is whether the soda is caffinated or not. There is no point drinking non-caffinated soda. After I know a soda is caffinated, I need to see if I have enough money to purchase it. If I do have enough money, I’ll purchase the soda.
My decision making process fits a conditional statement. The act of purchasing a can of soda is conditional to whether it is caffinated and affordable. Indeed, every time an instruction needs to perform an action that is conditional to some condition, you can use a conditional statement. In my case, the pseudocode looks like the following:
Note how this pseudocode almost reads like English. There are a few points you should observe:
Sometimes, an algorithm has an action to perform when a condition is true, and it has another action to perform when the same condition is false. Consider your reaction when you get a graded midterm. If the result is good, you might want to perform “the dance of joy”, otherwise, if the result is bad, you might want to perform “the dance of sorrow”. If the result is not good nor bad, you might want to “look indifferent”.
Here is an extended conditional statement to express your logic when you get a midterm back.
Note how the lines containing “elsif” and “else” are lined up with the lines containing “if” and “end if”. Also, all the action statements are indented relative to the lines containing “if”, “else if”, “else” and “end if”.
It is important to realize that you select one and only one of “dance of joy”, “dance of sorrow” or “look indifferent” in this code. In addition, we first evaluate “grade is good”. We only evaluate “grade is bad” if the grade is not good. If the grade is not good, and it is not bad, only then we execute the statement corresponding to a simple “else”.
Sequences and conditional statements are useful, but neither can express the logic of repetitions. We use repetitions a lot every day. For example, you may tell you kid “you are not watching TV until you have finished all homework assignments!” Another example is “while the tire is under inflated, pump more air into it.”
Tire pumping with an air pump without an inline pressure gauge is a repetitive process. You need to check the air pressure first, then pump some more air if the pressure is too low. After you pump some air, you have to check the pressure again.
The pseudocode for this logic is as follows.
The important point here is that you need to check first. We don’t just assume a tire is under inflated and start pumping air.
In contrast to prechecking iterations, postchecking iterations check a condition after an action is performed. If the condition is satisfied, the iteration stops. Otherwise, the logic repeat the action.
An example of postchecking is the process of adding sugar for people who like to sweeten their coffee. After you pour coffee into a coffee mug, do you need to taste for sweetness first? No, we already know plain coffee is not sweet enough! That’s why in this “algorithm”, one needs to add some sugar first, then check to see if the coffee is sweet enough. If the coffee is not sweet enough, one repeats the process of adding sugar. This “add sugar, then taste for sweetness” process iterates until the coffee is sweet enough.
The pseudocode to express this “algorithm” is as follows.
Here comes the fun part of pseudocoding. It turns out that conditional statements, prechecking iterations and postchecking iterations are all statements! This means you can embed a conditional statement within a prechecking iteration. Now, who would think of such a convoluted algorithm?
Just consider our dish washing example. During the dish collection step, let’s say you put dishes into two sinks, depending on how greasy the dishes are. We need to modify our logic a little bit now. The new logic (for collecting dirty dishes) is as follows.
Now, we can start to see the importance of indentation. The indentation helps us understand how statements are nested. Because the indentation of the conditional statement is the same as that of “locate a dirty dish”, we know the conditional statement follows “locate a dirty dish”. Because both “locate a dirty dish” and the conditional statement are both more indented than the postchecking iteration, we know that for each iteration, both “locate a dirty dish” and the conditional statement must execute.
This nesting ability of pseudocode is very powerful and it allows the specification of very complicated logic with just simple statements, conditional statements, prechecking iterations and postchecking iterations.
We have just learned pseudocoding in this chapter. How useful is it? How can we practice it?
Pseudocoding is useful not only in computer programming, but also in everyday procedures and processes. Whenever you have a process, a procedure or a “method” that has a logical pattern, you can probably express it with pseudocode. For example, I can express a simple and inefficient way to sort playing cards as follows.
As you can see, pseudocoding is useful in non-programming tasks.
Although in most cases, a person knows exactly which object you are referring to, natural languages leave too much room for ambiguity. This is why we do not use pronouns. Instead we use variables to refer to objects used in a program.
This chapter begins with the discussion of variables, followed by a discussion of expressions. Expressions provide values, which can be used to change the content of a variable.
A variable is a named object, its value (also known as content) can vary during the execution of an algorithm.
That sounds awfully abstract, doesn’t it? For those who are mathematics inclined or experienced, variables in programming have about the same role as variables in algebra. For the rest of us, what exactly is a variable?
Imagine you are given a task to track the minimum and maximum value of a list of items. You may do this when you are shopping for cereal, just to have an idea how much the price (per oz.) can vary.
In order to perform this glorious task, your mind needs to keep track of two numbers, the maximum and the minimum. When you find a box of cereal with a price lower than the known minimum, you update the minimum to the low price. The update for the maximum price is similar.
Believe it or not, you have just used two variables!
Although the actual maximum and minimum prices do not change, what you know as the maximum and minimum prices vary as you evaluate more items on the shelves.
Let us follow up our price research example and express the logic in pseudocode.
While this logic works, it is rather verbose. We can introduce some variables and make this algorithm more concise.
By using the equal (=) sign and some concise variable names, we make the algorithm easier to read and closer to programming languages.
Now that we have seen an example using variables, let us discuss some more concepts related to variables.
A variable must have two properties. First, it must have a name. This “name” allows us to uniquely identify the variable from all other variables. Second, it always has a value. The value may change over time, but there is always one.
You can, to a degree, see variables as coffee mugs. Each mug has a unique name written on it so it is possible to identify each an every mug. A mug is a container, what it contains can change over time.
Variables have other properties. For example, the “lifespan” of a variable determines when a variable comes to exist, and when it ceases to exist. The “scope” of a variable, on the other hand, determines which part(s) of an algorithm can see a variable. These concepts are fairly abstract, and we don’t need to understand them at this point. We will revisit these two properties later.
An expression is a mathematical construct that operates on values to produce a result. Alright, that’s an abstract description. Let us look at some examples of expression.
2 × X + 20 is an expression. If X has a value of 5, the expression evaluates to a value of 2 × 5 + 20, which is 30.
(20 ≤ X) ∧ (X ≤ 30) is also considered an expression. The ∧ symbol means logical-and (conjunction). Unlike 2 ×X + 20, this expression evalutes to true if and only if X is between 20 and 30 inclusively.
I am choosing the mathematical notation rather than a notation borrowed from a programming language. It is rather simple to map the notations once you learn a programming language.
However, you should know that most programming languages use + for addition, - for subtraction, * for multiplication (× in mathematical notation) and / for division (÷ in mathematical notation).
We will use mostly just addition, subtraction, multiplication and division in this course. Occasionally, we may use exponent. I assume you are familiar with all of these numerical expressions.
Comparitive expressions differ from numerical expressions because they do not produce numerical values. Instead, comparitive expressions produce boolean values. This means comparitive expressions produce results that are either true of false.
We will use the standard notations:
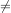 for inequality
for inequality
Logical expressions take one or two boolean values and evaluate to a boolean value themselves. We will take a closer look at the most commonly used logical expressions.
Negation means turning true to false, and turning false to true. The mathemtical symbol is ¬. For example, another way to say X ≤ Y is ¬(X > Y ). Occasionally, you also see people using the overline to mean negation, making X > Y equivalent to ¬(X > Y ).
Conjunction is simply “and” in English. For a conjunction to be true, both sides of the conjunction must be true. Otherwise, a conjunction evaluates to false.
For example, “Tak is tall and handsome” is true if and only if Tak is both tall and handsome. If Tak is short, no matter how handsome he is, the statement is still false. Similarly, if Tak is not handsome, the statement is false no matter how tall he is. It goes without saying, the statement is false if Tak is short and not handsome.
Conjunction is denoted by the ∧ symbol in mathematics.
Disjunction is simply “or” in English. For a disjunction to be true, at least one of the two sides must be true. If both sides of a disjunction are both false, the result of disjunction is false as well.
For example, “all-wheel-drive or chained” is true if a vehicle has all-wheel-drive, chained, or all-wheel-drive and chained. For a unchained front-wheel-drive vehicle, the statement is false because it is neither all-wheel-drive nor chained.
Disjunction is denoted by the ∨ symbol in mathematics.
Although all sound alike in English, they are not identical in logic. This little section discusses the differences among these three constructs in logic.
If Let us consider the following statement:
If the sky is orange, earthworms will fall from the sky.
“the sky is orange” ⇒ “earthworms fall from the sky”
This statement can either be true or false. This statement is true in the following cases (at least in logic):
The statement is false only in one case: when the sky is orange and earthworms do not fall from the sky.
In other words, the statement is stating that “the sky is orange” is a sufficient condition for “earthworms falling from the sky” to happen. The statement does not state anything about what happens when the sky is not orange.
Only If Let us modify the sentence a little bit:
Only if the sky is orange, earthworms will fall from the sky.
“the sky is orange” ⇐ “earthworms fall from the sky”
By inserting “only” before the word “if”, the meaning of the statement changes. For this statement, the following cases make the statement true:
The only case in which the statement is false is when the sky is not orange, and earthworms still fall from the sky.
In other words, this statement is stating that “the sky is orange” is a necessary condition for “earthworms falling from the sky”. There may be other necessary conditions for earthworms to fall from the sky. Therefore, just having the sky being orange does not automatically lead to earthworms falling from it.
If and only If Let us now consider the last case:
If and only if the sky is orange, earthworms will from the sky.
“the sky is orange” ⇔ “earthworms fall from the sky”
Two cases make this statement true:
Two cases make this statement false:
In other words, the statement states “the sky is orange” is both necessary and sufficient for “earthworms falling from the sky”. Put more plainly, assuming the statement itself is true, because “the sky is orange” is sufficient, an orange sky always leads to earthworms falling from it. On the other hand, because “the sky is orange” is necessary, a non-orange sky cannot possibly have earthworms falling from it.
Let us consider more about the ”ifs”.
If Tom breaks a window, he gets spanked. This means breaking a window is sufficient to get spanked. This statement does not say anything whether there exists or what other conditions can lead to spanking. Just breaking a window is enough reason to get spanked. But Tom can, for example, get spanked for setting the house on fire without breaking a window.
Only if Tom breaks a window, he gets spanked. This means breaking a window is necessary to get spanked. This statement leaves the possibility of needing other reasons in conjunction with breaking a window for Tom to get spanked. That is, it is possible that Tom breaks a window without getting spanked. This statement also means that seeing Tom getting spanked automatically implies a window is broken.
If and only if Tom breaks a window, he gets spanked. This means breaking a window is both necessary and sufficient for Tom to get spanked. This means Tom get spanked for sure after breaking a window, but there is no other reason to spank Tom. For example, you cannot spank Tom if he sets the house on fire if this statement is to remain true.
It is useful to be able to factor numbers into their prime factors. For example, 54 can be rewritten as 2 × 3 × 3 × 3. This is useful when you are computing with fractions.
In this example, we want to write an algorithm that factors a given number into its prime components. Let us assume that we just want to output the prime factors and leave it up to the user to utilize the factors. Given the number 54, the program should output 2, 3, 3 and 3.
For algorithms that solve simpler problems, it helps if you try to solve the problem by hand several times before attempting to write it in pseudocode. In our case, we can factor a number by hand to learn the general approach of factoring.
Let us consider 54. The manual factoring yields the following steps:

In other words, every time we find a prime factor, we subtract that from the remaining number, then try to factor the remaining number again. This process repeats until the number to factor is 1.
From the example, we know the overall code is iterative (it is a repetition). What condition makes us stay in the loop? How do we exit the loop?
It seems like we should exit the loop when the number to factor is 1. This is because 1 has no factor except itself. The next question is, then, whether we should use a pre-checking loop or a post-checking loop.
Let us think about what should happen when the algorithm is presented with a value of 1 to factor. Should the program say “1” as the output (the factor of 1 is 1), or should the program not generate any output at all? Technically, 1 is a factor of itself, so it should be printed.
This means we have to go to the iterations at least once. A post-checking loop allows us to do it.
Now, let us assume the number presented to the algorithm has a name of n. We have the following crude algorithm:
|
What we have done is to make a bold assumption that we already know how to find a prime factor f of n. Given this assumption, we should still check that this pseudocode works. I will leave the trace of this program to you.
Finding a prime factor of a number turns out to be an uncommon task. In other words, most programming languages/environments do not have a built-in method to do this. This means we have to find out how to do this and present it in pseudocode.
Note that we can now focus on the task of finding a prime factor of a number n. The overall code is already done in the previous step. In other words, we no longer need to worry about when to exit the loop that prints a factor for each iteration.
Let us use another example so we know how we find a factor of a number. This time, let us consider a more difficult case so we really have to think about it. Let us try to find a factor of 143.
How do start the process? You do not just randomly try different numbers (I hope not). Most people know that 2 cannot be a factor because the least significant digit (rightmost digit) is not a multiple of 2. How about 3? How about 4? How about 5?
A computer cannot easily tell that “the rightmost digit is a multiple of 2”. Therefore, it cannot use this rule that is easy for people to follow. A computer needs to start testing at 2. In other words, our algorithm should try 2 as a factor, then 3, then 4, then 5. We try these different numbers until one of two conditions becomes true.
For the number 143, when we try 11, we realize that (143 mod 11) = 0. This is great because this tells us that 11 is a factor of 143 and this task of finding a factor is done. What if we are trying to factor 13, when do we stop?
Obviously, if we try all the numbers from 2 up to but excluding 13 and still cannot find a factor, 13 is its own factor (because 13 is a prime number).
Overall speaking, we have to try consecutive numbers for as long as the number being tried is not a factor and the number being tried is less than the number being factored. “Trying consecutive numbers” suggests that we should use repetition, but which type should we use?
As it turns out we can use either, depending on which number we initialize f to. Our algorithm to scan for a possible factor can be a pre-checking loop:
Alternatively, we can use a post-checking loop:
After the loop exits, we are not done yet. If the loop exits because f is a factor of n, we can declare the f is a factor of n. However, if the loop exits because f ≥ n, we have to say the n is its own factor. This is the case because n may have a value of 1. If f is to store a factor of n after the algorithm we need to append the following code to one of the previous loops to interpret the exit condition.
Given a number n, how can we find a factor f for it? In order to do this, we need to rely on the modulus operator. Different programming languages use a different symbol for this operator, I will use the word mod to represent modulus.
The modulus operator requires two numbers. The number to the left is divided by the number to the right. The result of modulus, however, is not the quotient of the division. Instead, it is the remainder of the division. As an example (33 mod 7) = 5 because the remainder of 33 ÷ 7 is 5.
The modulus operator is useful in determining whether a number is a factor of another number. For example, let f be a number that may be a factor of n, and we need to determine whether it is a factor or not. If and only if f is a factor of n, the remainder of n ÷ f is zero. In other words, f is a factor of n ⇔ (n mod f) = 0.
Integrating all of this, the final code to find a factor f of n is as follows (using the pre-checking loop):
|
Our previous algorithm can be refined. It is true that, for a number n, if we cannot find a factor (other than 1) that is less than n, n is a prime number (so its only factor, other than 1, is itself).
However, this means in order to find out 37 is a prime number, we need to test numbers (as possible factors) from 2 to 36. This may not sound like a lot of numbers, but when we need to factor larger numbers, this approach becomes cumbersome.
Instead of just stating the refinement, let me pose this question. Given a number n that has a product of f and g, can we guarantee that at least one of the squares of f and g is less than or equal to n?
In mathematical terms, given the n = f * g, can we guarantee that ((f × f) ≤ n) ∨ ((g × g) ≤ n)?
For instance, let us assume n = 35. We can find two pairs of factors: 35 = 1 × 35 and 35 = 5 × 7. In the pair of 1 and 35, the square of 1 is less than or equal to 35. In the pair of 5 and 7, the square of 5 is less than or equal to 35.
For n = 49, we can find two pairs of factors: 49 = 1 × 49 and 49 = 7 × 7. Obviously, for the first pair, the square of 1 is less than or equal to 49. For the second pair, the square of 7 is still less than or equal to 49.
It turns out, as can be proven by contradiction, that we observation is true for all positive integers. In concise mathematical terms:
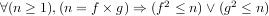 | (4.9) |
In English, this is saying “for all n that is greater than or equal to one, if n = f ×g, the square of at least one of the f or g is less than or equal to n”.
What is the big deal here? It turns out this little theorem allows us to refine our algorithm so we only need to search for a factor up to a number f such that f × f ≥ n. Our algorithm now becomes the following.
|
The difference is that we replaced the original condition f < n with f × f < n. The significance is big when n is prime. For example, for 41, we used to have to check possible factors from 2 to 40. Now we only need to check possible factors from 2 to 7. We’ll get back to this example later when we discuss the “complexity” of an algorithm.
Whew, up to this point, this chapter sounds more like a chapter out of a mathematics textbook rather than one for beginning programming! Although some may disagree, I think mathematics and programming are very tightly related. Having a strong mathematics background certainly does not hurt in programming.
However, let us focus on the process of writing this algorithm Particularly, notice how we just assumed there is a method to find a factor f from a given number n in algorithm 4.1. This is the application of the top-down technique. Essentially, I assumed there was an existing algorithm to perform an action. This assumption allowed me to focus on the overall logic of the original problem.
After I finished the overall algorithm, then I found out there was no existing algorithm for finding a factor. Only then did I have to worry about the logic of finding a factor. This eventually led to algorithm 4.2, which was later refined to algorithm 4.3.
Of course, there is more to programming than making assumptions that certain operations are already provided. Let us rewind and review the process of writing the factoring algorithm.
Every algorithm has an objective. It is important to know what the algorithm is provided with, and what the algorithm is supposed to generate/output/derive as a result. Without a clear understanding of the objective of an algorithm, you may waste hours to effort only to find out your algorithm does not do what is required of it.
The objective of an algorithm can be specified very formally and mathematically. For our class, however, we will generally use English statements that contain mathematical symbols when they are appropriate.
When you write an algorithm, you need to focus on the “type” of behavior that you need to handle. Some processes, such as washing dishes, can be separated into big sequential steps (collect, wash and rinse). Sequential steps are the easiest ones because one step simply follows the previous one.
The next main type of behavior is conditional statements. One or more conditions are used to determine which one out of many alternative actions should take place. In other words, conditional statements “map” conditions to actions.
The last main type of behavior is iteration (repetition) statements. These statements provide behavior that is repetitive. Although there are situations where the repetition does not stop (endless loops), most repetition terminates at some point.
Every behavior pattern fits into one of the three mentioned types. The following subsections point out important issues for each type.
It is important to remember that in a sequence, the order is important. If a step depends on the result of an earlier step or earlier steps, it must follow the step(s) that it depends on. Each step in a sequence can be an assignment statement, a conditional statement, a loop or the utilization of some abstraction operation.
A conditional statement associates conditions (logical expressions that evaluate to either true or false) with actions. It is important to remember that in the case of a conditional statement with “else if” components, the order of the conditions is significant. The algorithm evaluates the conditions in the specified order (top to bottom) until a condition evaluates to true or it executes the “else” statement if one is provided.
In other words, it is okay to write the following algorithm:
Note that when the algorithm evaluates the condition x ≤ 0, we know that x < 0 must be false already! In other words, if the algorithm prints “x is zero”, we know that ¬(x < 0) ∧ (x ≤ 0), which means x = 0.
Generally speaking, it is not a good idea to write programs like this example.
Loops are very important, and they are also a little difficult to specify. If you know that you need some form of repetition, you know you need at least one loop. Here is the various factors you need to consider.
What does the loop require (before the first iteration)? Are there any variables to initialize?
What condition is required to stay in the loop? Alternatively, what condition is required to exit the loop?
Is it possible not to iterate even once? If so, you probably need a prechecking iteration. Does the exit condition depend on the iteration itself? If so, you probably need a postchecking iteration. Certain algorithms can use one or the other.
What does the loop do per iteration? How does this relate to the exit condition or stay-in-loop condition? Do we know that each iteration can affect the exit condition so eventually we can exit the loop?
Let me give you an example. Let’s say we want to write a program to print numbers from 0 to 9. Let us name the variable containing the number to print n.
We know this algorithm is a loop because we have to print several times (repetition). Our pre-loop condition is that n should start with a particular value. The first number to print is 0, so we should initialize n to 0. n ← 0 becomes the initialization before the loop.
What is the exit condition of this loop? When n is greater than the 9, we are done! Perhaps the exit condition is n > 9. We’ll revisit this later.
What does each iteration of the loop do? Well, we need to print n. However, “print the value of n” does not affect the condition n > 9. If n begins with zero, it remains zero, and n > 9 is always false! The algorithm prints zeros forever.
Since we want the algorithm to print consecutive integers, we need to update n so its value become the next integer. This is done by n ← n + 1. Great, not only does this solve the problem of printing zeros, it also solves the problem of “forever”! Since the value of n is incremented for each iteration, it will become greater than 9.
We are almost done. We still need to decide the sequence of steps in the loop. Should we increment first, or should we print first? Recall that n is initialized to 0. If we increment first, the first integer printed is 1. This is wrong. We have no choice but to print n first, then increment n.
We are almost done. We need to decide whether to use a prechecking loop or a postchecking loop. As it turns out, we can use either one. This is because this algorithm requires at least one iteration, and each iteration affects the condition that determines whether to iterate or exit.
The postchecking loop (using the exit condition) is probably the more intuitive one:
In order to convert this to the prechecking loop, we have to negate the exit condition so it becomes the stay-in-loop condition:
The top-down design process does not tell you how abstract or detailed each “level” should be. In general, it is better to be more abstract than detailed. In other words, it is better to assume there are existing algorithms to perform more complex operations.
It is important to keep in mind why we need to keep each level relatively abstract and not crawling with details. Legibility is the key criterion when it comes to the selection of abstraction level. Some people can keep track of a single piece of pseudocode that is more than 50 lines with statements nested more than 4 levels deep. Most programmers can effectively handle up to about 20 lines and 2 to 3 levels of nesting. Beginners may want to limit to 7 to 15 lines and 2 levels of nesting.
We may not be able to choose the right level of abstraction the first time. This is okay. As soon as you realize your pseudocode algorithm is lengthier or contains more levels of nesting than you can effectively handle, increase the level of abstraction! Make assumptions about bigger chunks of steps. In other words, become more greedy, optimistic and lazy (the right way).
When you make an assumption of a “provided operation”, be specific about what information you need to provide it and what information it returns to you upon completion. For example, the abstract method “find factor f of number n” requires a given number n, and it computes a result f that is a prime factor of n.
This definition of interface is not only useful to clarify the input and output of the assumed provided operation, but it is always useful when you realize the assumption (of provision) is wrong and you need to write an algorithm to do it. The definition of interface becomes the objective of the wrongfully-assumed-provided operation.
Atomic variables are useful, but they are insufficient for some algorithms. For example, consider an algorithm that sorts a series of numbers, or to search for a number among a series of numbers.
In this chapter, we introduce the concept of arrays. Arrays are “aggregate” objects that can be broken into smaller components.
An array is a collection of objects of the same type, each is identified by an index number. Index numbers must be sequential integers.
Let us use an analogy. If you consider a mug is a number variable in a program, an array is like a boxful of mugs. The box itself has a name (a variable can be an array), but each mug inside the box does not have a name. Instead, the individual mugs are uniquely identified (from each other) by an integer. For example, the first mug in the box may have a number 0, the next mug may have a number 1 and etc.
The notation of an array is the same as any other variable, just a name. For example, x can be the name of an array of integers. Each element in an array, is “indexed” by an integral index. The item with an index of 2 in array x is denoted by a subscribe: x2 in mathematics. Most programming languages, however, use the notation x[2] to denote the element with an index 2 in an array called x.
It is important to realize that in computer programming, indices start at 0, not 1. In other words, the “first” item in an array has an index of 0, the “second” item has an index of 1 and etc. Consequently, it is not a good idea to say “first”, “second” and etc. It is more precise to say “item at index blah”. Languages such as Pascal, C, C++, Visual Basic (for the most part), Perl, PHP, Java, Javascript all use this convention of starting with index 0.
Most algorithms for arrays involve some kind of loop. This is natural because in order to perform any operations for items in an array, manually coding everything becomes insanely tedious.
Let us assume a is an array of n items (this means the index of the last item is, you got it right, n - 1!). We want to see if at least one of the numbers in a has a value of v.
Before you read any further, you should try to solve this problem. Imagine how you will do this in real life. Given a pile of cards with numbers, how do you find the card with a particular value?
Once again, we should construct this algorithm step-by-step. First, we choose the control construct at the top level. Should it be a plain sequence, a loop, or a conditional statement? On a loop has the open-ended property to perform operations for an entire array. We know we need a loop.
Next, we try to visualize what needs to be done in the loop. For each iteration, we need to check if the current card has the value we want to find. If not, we flip to the next card and check the condition again. In other words, one may enumerate the operations as follows:
This little sequence (of operations) suggests that we should check the condition first. A prechecking loop can do this. We have the first cut of our algorithm, mostly in English:
Let us try to map this everyday pseudocode to our more formal pseudocode. How do we designate the value of an element in an array? We need an index. For example, a0 is the first element in the array. However, we cannot use a constant for the index because we need to “flip to the next card”, which translates to incrementing the index. As a result, we need a variable to act has the index of the “current card”. Let us call this index variable i. Recall the value we are searching for is in variable v. Our new “formal algorithm” becomes the following.
How do we flip to the next card? Assuming there is no particular order you need to search through the cards, we can start with index 0, then increment the index (by one) for each iteration. Since i is the index variable, this means we need to increment i in the loop:
We have handled the core logic of this algorithm. Several issues still prevent this from working. What is the first value of i before we execute the loop? Where do we start searching in this pile of cards? Since we are incrementing i in the loop, we should start with the first card in the pile. This translates to an index of zero as a starting point. To make sure the algorithm starts with an index of zero, index variable i should be initialized to 0. This requires adding an initialization of i before the loop.
We are almost done. The next issue is one that the real-life example does not make obvious. When you search for a value from a pile of cards, what do you do when you have search all cards and still cannot find a card with a particular value? You simple realize there is no such card and quits. This quitting logic is very “intuitive” and is often missed in programming.
In our current program, if none of the elements in a has a value of v, what happens to the algorithm? Our program does not exit! Instead, it keeps incrementing the value of i (so that i ≥ n) and try to compare non-existent elements of a to v. While this logic is wrong in pseudocode, if it is translated to actual program code, it often leads to crashes.
What we need to do now is to somehow have the loop exit not only when it finds an element in a with a value v, but also
when i is no longer a valid index. i is a valid index when 0 ≤ i < n. We don’t need to check if 0 ≤ i because i starts with 0, and
all we are doing is to increment it. As a result, we can simply check that i < n to stay in the loop. This is a condition that
needs to be true in addition to the original stay-in-loop condition of ai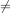 v. Our algorithm now becomes the
following.
v. Our algorithm now becomes the
following.
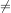 v) do
v) do
While this code works in most programming languages, it work only because of an implementation trick called “lazy evaluation”. Read the section to find out what it is.
Are we done? In a sense, yes. We have a loop that exits as soon as it find an element in a that has the same value as v, it also exits if no such element can be found. However, the result from the search is not utilized. After the loop, we need to determine whether at least one element in a has a value v.
This is done by analyzing the post condition of the loop. We need two conditions, ai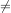 v and i < n to be true to stay in the
loop. As a result, we exit the loop as soon as one of the these two conditions evaluate to false. In other words, when the loop
exits, we know that ai = v or i = n.
v and i < n to be true to stay in the
loop. As a result, we exit the loop as soon as one of the these two conditions evaluate to false. In other words, when the loop
exits, we know that ai = v or i = n.
Given this fact, it is easy to conclude whether an element in a has a value of v. If and only if i = n, there is no element in a that has a value of v. We add this logic to the algorithm to conclude it.
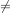 v) do
v) do
You can try this algorithm with a small array. It does work!
Let us revisit the algorithm to find a element in an unsorted array a with value v. The algorithm is as follows:
The stay-in-loop condition, (i < n) ∧ (ai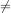 v), is tricky. The question is do we always evaluate both sides of the conjunction,
or do we quit as soon as the left one evaluates to false? Afterall, we only need at least of them to evaluate to false in order for the
entire conjunction to evaluate to false.
v), is tricky. The question is do we always evaluate both sides of the conjunction,
or do we quit as soon as the left one evaluates to false? Afterall, we only need at least of them to evaluate to false in order for the
entire conjunction to evaluate to false.
In languages like C, C++ and Java, that’s exactly what happens. Such languages are known to have “lazy” logical operators because they do not evaluate a condition unless it is necessary. Other languages, such as Pascal, evaluates both conditions of a conjunction, even if the left one already evaluates to false!
This “hard working” behavior poses a problem. If i < n is false, i ≥ n. This makes the comparison ai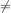 v meaningless because
there is no such element as an!
v meaningless because
there is no such element as an!
For such languages, the algorithm must be adjusted so the check for i < n is not in the same conjunction
as the check for ai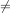 v. This is often done with the introduction of a boolean variable. Our algorithm can be
modified as follows to avoid the “hard working” logical operation problem. For ease of reading, read b as “element
found”.
v. This is often done with the introduction of a boolean variable. Our algorithm can be
modified as follows to avoid the “hard working” logical operation problem. For ease of reading, read b as “element
found”.
|
given a is an array with n numbers
given we want to find an element in a with value of v given b is a boolean variable b ← false i ← 0 while ¬b do if ai = v then b ← true else i ← i + 1 if i ≥ n then b ← true end if end if end while if i = n then conclude that no element in a has a value of v else conclude that ai = v end if
|
The previous algorithm cannot be made much more efficient for searching in an unsorted array. However, if an array is sorted, we can improve the efficiency. This section discusses two methods to search for a value in sorted arrays. Let us assume the given array is sorted in non-decreasing order.
Refer to algorithm 5.1. Although this algorithm works for sorted arrays as well as unsorted array, it can be made more efficient. Consider the following instance (we want to search for 50):
| index | value | comment |
| 0 | 2 | 2 < 50, maybe another element matches 50 |
| 1 | 6 | 6 < 50, maybe another element matches 50 |
| 2 | 23 | 23 < 50, maybe another element matches 50 |
| 3 | 56 | 56 > 50, no further element may match 50! |
| ... | ... | no need to look at these elements |
What this means, in formal terms, is that for a sorted array a, ai > v implies aj > v for all j greater than or equal to i. This also means that we need to look further only if ai < n.
Our prechecking loop can change it condition so it reads as follows,
This change impacts how we interpret the conditions after the loop exits. In algorithm 5.1, the condition i = n indicates the number is not found. Once we perform our modification, the loop can exit before i = n as soon as ai ≥ v. This means either i = n or ai > v can indicate that value v is not found in the array.
After all the modifications, our algorithm is shown as follows.
|
given a is a sorted array with n numbers
given we want to find an element in a with value of v i ← 0 while (i < n) ∧ (ai < v) do i ← i + 1 end while if (i = n) ∨ (ai > v) then conclude that no element in a has a value of v else conclude that ai = v end if
equential search using lazy evaluation for a sorted array. |
On the average, this modified method only needs  iterations to conclude that a value v does not exist in the array. By
comparison, the original algorithm (5.1) requires n iterations.
iterations to conclude that a value v does not exist in the array. By
comparison, the original algorithm (5.1) requires n iterations.
Given a sorted array, an even better trick is called “binary search”. This approach maintains a range of the array in which a value v may be contained. For each step, this algorithm finds the middle (or approximately the middle) element in the current range. Based on the comparison of this element with v, the algorithm either matches v, rules out all elements before, or rules out all elements after.
Observe the following example (to search for 16):
| i | ai | pass 1 | pass 2 | pass 3 |
| 0 | 2 | ruled out | ruled out | ruled out |
| 1 | 5 | ruled out | ruled out | ruled out |
| 2 | 7 | ruled out | ruled out | ruled out |
| 3 | 13 | 13 < 16 | ruled out | ruled out |
| 4 | 15 | 15 < 16 | ||
| 5 | 19 | 16 < 19 | ruled out | |
| 6 | 25 | ruled out | ruled out | |
| 7 | 31 | ruled out | ruled out | |
In pass 1, the middle element is a3, which is less than 16. Because a is sorted, this means aj for j = 0,1,2 must be less than 16 as well. We can rule out a0 to a3. In pass 2, we find the middle element of the range a4…a7, a5, and compare it to 16. Since a5 = 19 > 16, we conclude that a6 and a7 cannot be 16, either. In pass 3, Our last availble element, a4, proves to be different from 16. Now we can conclude that 16 does not exist in the array.
Is this algorithm a sequence, a conditional statement or a loop? Because we need to find the middle element repeatedly, this must be a loop.
Now that we know we have a loop, what does each iteration do? Each iteration of this loop locates a middle element in the remaining range of the array. This element is compared to the value v. If there is no match, the result is used to rule out about half of the remaining range of the array.
How do we exit the loop? When the “middle element” has the same value as v, we exit the loop. Also, when there is no more available element to match (because everything is ruled out), we also exit the loop.
Should this be a prechecking or postchecking loop? Even if we are very lucky, we still need to find one “middle element” to match in order to conclude that v is in the array. This means the loop needs at least one iteration. We should use postchecking (repeat-until).
A rough representation of the algorithm is given as follows:
How do we keep track of the range of the array that may contain v? We can use a variable f (for first) to maintain the lower bound of the index. We can also use another variable l (for last) to maintain the upper bound of the index. At any time, v may match aj for all f ≤ j ≤ l.
Initially, we know nothing about the array. As a result, every element in a may match v. f should start with 0 and l should start with n - 1.
Given f and l, the midpoint index is the average of these two variables. In order to make sure the midterm m is an integer,
we define m = ⌊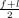 ⌋.
⌋.
If am < v, it implies that aj < v for all j ≤ m. This means we can move the lower bound to m + 1.
If am > v, it implies that aj > v for all j ≥ m. This means we can move the upper bound to m - 1.
When f > l, there is no element aj such that f ≤ j and j ≤ l. This means f > l implies all elements of a are ruled out.
After we formalize the algorithm, we have the following,
|
given a is a sorted array with n elements
given v is a number to search for in a f ← 0 l ← n - 1 repeat m ←⌊ 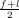 ⌋ ⌋
if am < v then f ← m + 1 else if am > v then l ← m - 1 end if until (f > l) ∨ (am = v)
|
This assignment is broken into three parts. The first part is to write an algorithm (in pseudocode) to find the maximum number in an unsorted array. In other words, given an array a with n items, find the element in the array with the maximum value. You are guaranteed that elements have unique values (no two elements of a have the same value). Store the maximum in a variable called w. This should involve a loop and a variable i to keep track of the index of the “current” element.
Once the first part is done, modify the algorithm just a little bit so that the maximum stored in w is less than a given value, v.
Once the second part is completed, you can finish the last part. Modify the algorithm so that given an array a with n elements, find the largest m elements and store these in another array x. Obviously, m < n. You will need an outer loop to include your existing pseudocode. Use a new variable j to keep track of the current element in x. In addition, you need to somehow use xj in place of v. This means you should not need or use v anymore.
Given an array a with elements of value 2, 4, 1, 61, 52 and 23, the largest three elements (stored in x) are 61, 52 and 23.
Turn in the pseudocode for all three algorithms.
The due date is two weeks from 03/10/2004.
Send it as an attachment to tauyeung@drtak.org. The subject of the email should be as follows:
CISP300 Assignment 2
|
.
I can open practically all word processing files except Word Perfect files. Plain text is fine with me as long as I understand the code.
Assume that array a is sorted in a non-decreasing fashion. In fact, make the following assumption about the content of a, an array of 10 elements:
![a[0] = - 3 (6.1)
a[1] = 2 (6.2)
a[2] = 2 (6.3)
a[3] = 5 (6.4)
a[4] = 6 (6.5)
a[5] = 10 (6.6)
a[6] = 15 (6.7)
a[7] = 15 (6.8)
a[8] = 100 (6.9)
a[9] = 2000 (6.10)](book19x.png)
Perform a trace for each of the following values of v:

Present the trace of each test case as a table. In this table, use the following columns:
The length of your trace table depends on the test case.
Send the document (Word .doc, .rtf, OpenOffice .sxw or plain text .txt) to me at tauyeung@drtak.org. The subject of the message must say
cisp300 project1 by your name
|
Replace your name with your actual name. Submissions not following this rule will be deducted 50 points!
Subroutines have two main purposes. The first one is already discussed: a subroutine allows its “consumer” to simplify the overall logic so the details can be abstracted/hidden. The second purpose of subroutines is to allow the sharing of code.
For example, let us consider the example of writing a program that prints a range of number between 1 and 100 inclusively. We want to let the use specify the first number and the last number, but the last number should be greater than or equal to the first number. The tedious version of the this code is as follows:
Although the core logic of this code is simply to print the numbers in a loop, the error checking logic for both the first and the last number of the range is tedious and makes the pseudocode difficult to read. This means they are good candidates for abstraction.
In addition, also notice how the logic to input the first number resembles the logic to input the last number. Maybe we can use one subroutine pretend that we do have one subroutine called “bound_check_read” to do read a number within a maximum and a minimum. We new code becomes the following:
Hey, not only does our code is easier to read without the clutter of the bound checking logic, it seems like we only have to define this bound_check_read subroutine once, even though it is utilized twice!
Of course, nothing is free, but the benefits of subroutines are almost free (compared to the hassle to create them)!
A subroutine can have many components. This subsection discusses the components of a subroutine.
The name of a subroutine is required. It must be unique so the subroutine can be distinguished from all other subroutines. Because we are using pseudocode code in this class, any name can be used. For a real programming language, however, subroutine names usually have to be restricted by some rules.
A subroutine can have option parameters. Parameters are pieces of information either supplied to or returned by a subroutine. We will talk about this a little more later.
Local variables of a subroutine is visible only within the subroutine. Such variables cannot be seen or accessed from outside the subroutine. The advantages of using local variables include the ability to reuse popular names in different subroutines.
A subroutine should have some code associated with it. This code can be “invoked” by other portions of the program. The code defined for a subroutine has access to formal parameters as well as local variables.
Formal Parameters represent pieces of information that is either given to the subroutine or should be returned by the subroutine. In our example, “bound_check_read” requires two given numeric values (the minimum and the maximum), while it returns a number that the user enters that is between the minimum and the maximum.
It is important to keep in mind that formal parameters are seen from the perspective of the subroutine itself, not from the perspective of whoever wants to invoke the subroutine. In other words, if a subroutine is like a small office (in which there is an operator) to perform a certain task, the formal parameters are the labeling of the in and out slots from the inside of the office.
Instead of using the in/out slot concept (names of formal parameters are not visible from outside a subroutine), some languages use the in/out tray concept, which makes the names of the formal parameters visible from outside a subroutine. For clarity, we use this second approach (tray) in this class.
There are two main types of formal parameters, “given” and “provide”. An “given” parameter is given to the subroutine, while a “provide” parameter is something to be returned/replied to whoever invoked the subroutine. In some cases, a formal parameter can be both “given” and “provide”.
Our “bound_check_read” subroutine can be defined as follows:
In order to invoke a subroutine, it must be provided with all the formal parameters. In most programming languages, formal parameters of the definition of a subroutine are “instantiated” by actual parameters (also known as arguments) in the order of formal parameter definition. In other words, the first argument goes to the first formal parameter, the second argument goes to the second formal parameter and etc.
This method results in more compact code (though not more efficient), but it is also more confusing for beginners. In this class, we “instantiate” formal parameters with explicit symbols.
For example, if we want to read a number between 1 and 100 into our variable f, we use the following statement:
Verbose? Absolutely. Clear? Yes! We use → to pass a value (on the left) to a “given” formal parameter (on the right). We use ← to store a provided value (on the right) to a variable of the invoker (to the left). For formal parameters marked “given and provide”, we use the ↔ with the invoker’s variable on the left and the formal parameter on the left.
In other words, we always specify the formal parameter on the right of →, ← or ↔.
For example, we can define a simple subroutine to increment a number:
Whenever we need to increment a variable, say x, we use the following statement:
In most programming languages, these parameters are also known as “passed by value”. Parameters that are “given only” or “passed by value” are copies of the actual arguments. This means that the subroutine can make changes to the parameter, but the changes are only applied to copies of the arguments. The actual arguments are never modified.
Let us consider the following definition:
In this definition, x is incremented by 2. However, because x is a “given only” parameter, the changed value is only useable within sub1. Let us consider the following invocation:
This code prints 20 instead of 22. This is because parameter x is just a snapshot copy of myvar when myvar had a value of 20. When we added 2 to x, it only change the snapshot of myvar, but not myvar itself. As a result, the value of myvar was never changed by sub1.
If a parameter is marked either “provide” or “given and provide”, it belongs to the category described in this section.
In most programming languages, such parameters are called “passed by reference”. Parameters that are “provide” or “given and provide” are not copies of the corresponding arguments from the caller. Rather, they are “references” to or aliases of the corresponding arguments specified by the caller. It may be more intuitive to see such parameters as “aliases” (instead of “references”) if you do not have any programming experiences.
Let us consider the following definition, which is very similar to the one used in the previous section:
In this case, x is marked “given and provide”. This means that the initial value of x is given by the caller. More importantly, however, is that x is an alias of the argument specified by the caller. Whatever happens to x happens to the argument. When we add 2 to x, we are actually adding 2 to the argument that is “aliased” by x.
Let us consider an invocation of sub1:
This code prints 22 because when we added 2 to x when sub1 was invoked, we actually added 2 to myvar of the caller.
But wait, what if we have the following invocation?
In other words, can x be an alias of a constant 65? Or, even more interestingly, can we do the following invocation?
Most computer languages will mark the previous two invocations as errors. However, some languages allow them. Of course, in practice, it makes little sense. Since x is an alias of the actual argument, this means the subroutine is effectively doing (5 × 13) ← (5 × 13 + 2) in the second example.
It only makes sense to use something that can store a value on the left hand side of ←.
Unfortunately, languages like C++ and Visual Basic allows a caller to pass a non-storage parameter by reference. I will not go into the implementation detail that technically allows this to happen, but it suffices to say that intuitively speaking, it does not really make much sense.
The pseudocode for selection sort is as follows:
This is not a subroutine. I want you to write (more like copy, paste and modify) two subroutines. The first subroutine, let’s call that “sort”, is the overall subroutine. It is responsible to sort an array. However, this subroutine is too long. We want to break certain portions off to another subroutine. This sub-subroutine should implement the following:
You may call this subroutine “findmin”.
After you define subroutine “findmin”, don’t forget to change subroutine “sort” so that it invokes subroutine “findmin”.
For each subroutine, be sure to include the proper syntax to start and end the definition (of the subroutine), and clearly identify the category (given only, given and provides, provides and local) of each name used.
You have one week from 2004/10/25 to complete this project. Once you are done, send it to tauyeung@drtak.org with the subject line as follows:
cisp300 project2 by your name
|
Be sure to change your name to your actual name! 50 points will be deducted if this convention is not followed!
This chapter looks into the necessity of types and how we can create our own types.
The type of a value defines what a program can do with it. For example, if we say that x and y are of integer type, we know that we can multiply x and y (x×y resulting in an integer product), subtract x from y (y -x resulting in an integer difference) and etc. On the other hand, we cannot compute the conjunction of x and y (x∧y) because conjunction is an operation that only applies to true/false values.
This means we have implicitly used another type! What is the type of the expression x < y? This type is called “boolean”. Value of boolean type can have one of two values: true or false. Let us assume a and b are of boolean type. It makes sense to compute a ∨ b, (¬a) ∧ b and etc., but it makes no sense to compute a + b.
An analogy of typing is the old caste system used in the Middle Ages. The “caste” to which a person belongs defines what this person can and cannot do. Another analogy parallels a “type” to a “species”. For example, an animal of the species “fish” can swim and breathe under water. An animal of the species “reptile” can breathe air but has no automatical body temperature maintenance. “Fish” and “reptile” are the types in the animal kingdom.
In most programming languages, the type of a variable must be known and it must remain the same throughout the lifespan of the variable. This closely resembles the species of an animal in the animal kingdom because an animal must belong to a particular species from birth, and it cannot change its species during its lifespan. Few languages (mostly interpreted languages like Visual Basic and Perl) allow a variable morph from one type to another. For beginners, however, I suggest that we assume the type of a variable cannot change.
In summary, the type of a value defines what operations are applicable to the value.
Since we are now aware of the type of variables, we must be careful when we assume variables in our algorithms. For example, our factoring program should be modified so that the types of variables are clearly visible. While pseudocode has no particular syntax, we can use the following format:
An array is a aggregate of individual items. One of the properties of an array is that individual items in an array are accessed by their indices. Each index is an integer, the first index is 0, and all indices must be consecutive integers.
Now that we have introduced the concept of “type”, let us state another property of an array. All items in an array must be of the same type. All this means is that an array cannot contain some integers, some real numbers and then some boolean values. You can have an array of integers, an array of real numbers, and an array of boolean values.
The strength of array-aggregates is the ability to access individual items by their indices, and indices can be any expressions that evaluate to integer values. However, sometimes, it is useful to group items of different types into a single unit.
For example, let us consider a student’s record. Such a record, in real life, typically contains the following fields:
If we need to process student records with a program, it is helpful to have a aggregation that parallels a real life record. This way, we can handle a record as a whole most of the time, and only deal with the components whenever we need to.
For example, if we want to compare the GPAs of two students and print a statement to state who has a higher GPA, we can use the following code:
Let us take a closer look. The first part with record ...end record is the definition of “student” as a record. It specifies that a “student” record has two fields, the “GPA” field is a real number, while the “name” field is a piece of text. This definition let us know what a “student” record looks like. At the same time, it defines a new type with the name “student”.
In the pseudocode, we have two given variables a and b. Both variables are of type “student”. This means variable a has its “GPA” and “name” components, while b has its own components of the same name. Note how the comparison in the conditional statement only uses the “GPA” field, while the printing only uses the “name” field.
Let us use an exercise to illustrate why records are useful, and generally how it can be applied.
Recall our binary search algorithm in subsection 5.4.2. It is useful provided that an array is sorted.
Given an array of student records, it is helpful to sort the array by lastname-firstname (to quickly locate a student by name), but it is also helpful to sort the array by student number (to quickly locate a student by student number). Let us assume a student record is defined as follows:
Let us review the selection sort algorithm:
|
given a is an array of n elements
local i is an integer local m is an integer local j is an integer local t has the same type as an element in a i ← 0 while i < (n - 1) do m ← i j ← i + 1 while j < n do if am > aj then m ← j end if j ← j + 1 end while t ← ai ai ← am am ← t i ← i + 1 end while
|
We want to find a student record quickly by name as well as by student number. One way is to sort the number by the search criterion first, then perform binary search. The other method is simply to use the searching algorithm for unsorted array for one criterion.
Neither of these methods is fast. Ideally, we want to keep the array of student records sorted by name and student number at the same time.
How can we do this?
The answer is actually quite simple. We need to use two arrays in addition to the array of student records. These two additional arrays are arrays of integers.
The first array, let’s call it x, is an array of indices of student records that is sorted by student name. In other words, axp ≤ axq given that p is less than q. The second array, let’s call it y, is an array of indices of student records that is sorted by student number, ayp ≤ ayq given that p is less than q.
Now we need to modify the sorting algorithm so that we have one that sorts by student name, and another one to sort by student ID. We also need to modify the binary search algorithm so that we have one that searches by student name, and another one that searches by student ID.
Your homework assignment is to turn in two sorting algorithms and two binary search algorithms so that we have ways to keep the indices sorted, and ways to search by the indices. Name your subroutines “sort-by-name”, “sort-by-id”, “search-by-name” and “search-by-id”. For the sorting subroutine, it should have the following definition:
Turn this in by 2004/3/31 (Wednesday) by email. Send it to tauyeung@drtak.org with the following title:
CISP300 Assignment 3 by Your Name
|
Emails without the proper subject line can be lost, and I will deduct 40 points from it if it is not lost!
This homework assignment is worth 200 points.
The following is the solution to the selection sort algorithm modified to produce an array of indices.
For the binary search algorithm, change am to axm.name for search-by-name.
We can nest aggregate types. In other words, we can have an array of records, or we can include an array as a component of a record.
Let us consider an array of records. This may be used to represent a group of students (such as in a class). We can modify our binary search algorithm so we can search for a particular student in an array of student records sorted by the “name” field:
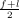 ⌋
⌋
What is am.name? Let us peel this onion:
Now that we have demonstrated how an array of records can be useful, the next section discusses how a record containing an array (as one of its fields) can be useful.
A “queue” is a British term for a line of persons waiting for something. It is also the official term for any data structure that has the first-in-first-out characteristics.
Let us consider the example of a carousel in-slot that is responsible for taking all incoming work to be done at a worker’s desk. For our discussion, let us assume the carousel has 8 slots to handle up to 16 buffered incoming work requests.
The worker uses a post-it to indicate the “next to process”. As the worker removes an incoming request from a slot, the post-it is moved clockwise by one slot. There is also a post-it to indicate “next request”. Anyone who wishes to place a work order must put the work request at the “next request” post-it, then move this post-it clockwise by one slot.
Figure 8.1 illustrates an initial configuration where there are two buffered requests (to be processed). Note how the “next to process” post-it is tagging the first filled (gray) slot clockwise, and how the “next request” post-it is tagging the first unfilled (white) slot clockwise.
After we process a request, we move the post-it to the next request (clockwise). Figure 8.2 illustrates the carousel after one request is processed.
If the worker process the only remaining request before any new requests come in, it becomes the one illustrated in figure 8.3. Note that in this configuration, both the “next to process” and “next request” post-its are on the same slot. This is how the worker knows there is no request to be processed at this point.
Let’s say lunch hour is over, and suddenly many requests come in at about the same time. More specifically, let us assume eight requests are received at about the same time before the worker can remove any one for processing. Our carousel is now filled. The “next request” is moved clockwise eight times. Figure 8.4 illustrates our 100% filled carousel.
Figure 8.4 also demonstrates how we know there is no more room for one more request. When the “next request” post-it is at the same slot as the “next to process” post-it, our carousel is filled up.
This also means it is not sufficient to just keep two post-its. We need to actually count the number of filled slots.
The carousel is our array! Imagine that we assign indices to each slot in the carousel. Figure 8.5 illustrates the numbering of the slots.
This means instead of using a post-it to tag a slot, we can use two indices (integers) to indicate which slot is to be processed, and which slot should receive the next request. That is, “next to process” and “next request” become two variables of integer type.
In order to represent a carousel, we can use the following record representation, after we rename “carousel” to its formal name, “circular queue”, “next request” to tail and use count to count the number of filled slots:
Note that we did not say specifically what a “slot” is. In other words, “slot” can be a simple type like integer, or it can a complex record or array all by itself. As far as the logic of a circular queue is concerned, the type of a slot is not important.
You can perform several operations for a circular queue. For example, we can initialize it, check if it is empty, if it is full, to remove the item at the “head” and to insert an item at the “tail”.
We will write some subroutines to handle each operation.
The following subroutine initializes a circular queue c.
As discussed earlier, checking for an empty circular queue only needs to check if the head and tail are the same. The following is the subroutine to do so:
This subroutine is rather simple. To invoke this subroutine to check if a particular circular queue x is empty, we use the following pseudocode:
The logic to check for a full circular queue is similar to the one to check for empty. We only need to compare the “count” field to 8 instead of 0.
The algorithm to add to the tail slot is as follows:
The invoke statement may look a little confusing. This is because the subroutine being called, “is circular queue full”, also has formal parameters c and result. The negation of result is necessary because “add to circular queue tail” provides a result of true if and only if it successfully add to the tail of a queue. If result is true from the invoke statement, it means the queue is already full and therefore the add operation fails. After the negation of result, result is true if and only if there is room to add to the circular queue.
The statement c.a(c.head+c.count) mod 8 ← s also deserves a little explanation. c.head is the index of the head of the queue. c.head + c.count is the index of the tail (next available slot). However, this sum can exceed 8 (e.g., when c.head = 7 and c.count = 3). (c.head + c.count) mod 8 ensures the number is between 0 and 7. This number is then used as the index for the array “a” (as a field) of a circular queue record c. The indexed element of this array is finally used as the destination so we can copy s (the intended contents of a slot) to a slot in the circular queue.
The algorithm to remove contents from the head of a circular queue is as follows:
This subroutine is similar to “add to circular queue tail”. result is a formal parameter to indicate whether a slot was successfully removed from the head of the provided circular queue. s is a formal parameter to contain the contents of the removed slot.
The only part that requires explanation is c.head ← (c.head + 1) mod 8. After we remove one slot from the head, the head must advance to the next slot in the carousel. However, we may be advancing from index 7 to index 0. This is why we need to use the modulus operator to ensure the resulting number (the next head index) is still between 0 and 7 inclusively.
Abstract data type is not a language feature of pseudocode or any programming language. Instead, it is a way of programming that helps to make programs less buggy and easier to understand.
In our circular queue example, any code in a program can access any field of a circular queue record. In other words, nothing prevents the following line of code:
The result of this statement, however, is profound. While there may be a reason to do this, it is, nonetheless, a dangerous statement. This is especially the case when a programmer accesses the internal structure of c throughout an algorithm. Why? What if we change the size of the array “a” of a circular queue to 20 elements? Code sprinkled everywhere may require modifications. What if we rename the “count” field of circular queue to “filled slots”? Code directly referring to “count” throughout the algorithm need to be modified.
Abstract data type is, as discussed earlier, a way of programming. It requires the programmer access a variable of a particular type only via a small set of subroutines.
In other words, if you treat “circular queue” as an abstract data type, you can only access it via one of the following subroutines:
You are no longer allowed to say c.count ← 0 whenever you feel like it. Instead, you have to invoke “initialize circular queue” to initialize a circular queue to an empty queue.
An abstract data type is “abstract” because to the consumer (someone who needs to use a carousel), it doesn’t matter any more how the carousel is implemented.
Let us consider an analogy. Televisions based on CRTs (cathode-ray tube) adjust brightness by changing the high-voltage charge at the electron gun. Televisions based on LCDs (liquid crystal displays), however, adjust brightness by altering the bias voltage to align liquid crystals. As a consumer who just want to change the brightness of your TV, do you care? To you, your remote control and on-screen adjustment menu form the abstract interface to all televisions, regardless of the actual implementation.
Similarly, as long as you (the consumer) only use the provided subroutines to access variables of type “circular queue”, I (the designer) can completely change the implementation from using an array to dynamically allocated memory and pointers without affecting your code in any way.
This isolation of usage from implementation is a result of using abstract data types.
Although abstract data type was useful in the organization of code and the containment of bugs, it has some limitations. One limitation is the inability to derive a type from another type. Let me give you an example to illustrate this.
Let us consider the type of a shape that a computer can draw. The simplest type is a pixel (picture element). A pixel only needs one screen coordinate. It has properties such as color and transparency. Subroutines that provide interfaces to a pixel include setting the color, setting the transparency, setting the coordinate and displaying the pixel on a window.
The next simplest type is a circle. A circle has all the properties and subroutines of a pixel, but it has the additional property of radius and the additional subroutine of setting the radius.
In abstract data type programming, not only is circle considered an entirely different type from a pixel, it also has its own subroutines to set coordiate, set color and display in a window. This means we need to use different names for the subroutines that are applicable to circles.
The biggest drawback, however, is now it is difficult to define a circular queue to handle drawing requests that may be pixels or circles. In the real world, there are also rectangles, triangles, arcs and etc. If you define a circular queue of pixel requests, it cannot store requests to draw circles and vice versa. Defining a circular queue for each type of shape is possible, but it means duplication of code as well as effort. In addition, it also becomes difficult to maintain the first-come-first-serve order when there are multiple circular queues.
This is one of the many problems that object oriented programming addresses. Let us look into object oriented programming in more details.
The most fundamental terms in object oriented programming (hence OOP) are “objects” and “classes”. Although both terms have broad meanings outside of programming, they carry very specific meanings in programming. This section explains these two terms in the context of OOP.
An object is something that has existence. For example, Tak the professor, Fido the dog, Sawteeth the shark are all objects. An object can have many properties. For example, Tak the professor has properties including gender, height, weight, degrees earned, social security number and etc. Fido the dog has properties including gender, height, weight, name of owner, length of tail, fur color and etc. Objects also have behaviors. Tak the professor can drive, teach, type classnotes, write questions for examinations and grade. Sawteeth the shark can breath in water, swim and bite.
Some objects have similar types of properties as well as behaviors. For example, let us consider ex-presidents (alive or dead). George Washington has a birthdate, presidency duration and a list of accomplishments during his term. Bill Clinton, another ex-president, also has a birthdate, presidency duration and a list of accomplishments during his term. Note that these two presidents do not have the same birthdates, presidency durations and etc., they merely have the same type of attributes or properties.
In fact, all ex-presidents have the same type of attributes listed above. By contrast, Tak the professor does not have (and will never have) the attribute of presidency duration. The fact that George Washington was an ex-president and Bill Clinton is an ex-president means they have an attribute of presidency duration.
“Ex-president” in this analogy is a “class”, while George Washington and Bill Clinton are “objects”.
In other words, a “class” is a collection of common attributes and behaviors that describe/define a bunch of objects. Another way to see this is that all objects of a particular class have the same set of attributes and behaviors, although each object has its own values for each property. The value of Bill Clinton’s presidency duration (property) is 1992-2000, while the value of George Washington’s presidency duration is 1789-1796.
The values of all properties of an object is also known as the state of an object.
At this point, you may be thinking, an object is a variable, a class is simply a type as discussed in the previous chapter. Well, you are almost right, but a class can do more!
The biggest notation change from type-oriented pseudocode to class-oriented pseudocode is where we indicate the type/class and whether the object being manipulated by a subroutine is explicitly represented or implicitly represented. Let us use shapes that a computer can draw as examples.
Using the type-oriented approach, the abstract data type “pixel” may have the following definition:
In the class-oriented approach, all subroutines that define the interface to a particular class (formerly known as record) are declared inside the definition of the class. As a result, the class definition of pixel is as follows:
The change may seem trivial and merely syntactic, but the change is in fact conceptual! Let us see why.
First of all, we changed the name of the subroutine from “set pixel color” to “set color”. This is done because the subroutine is now defined local to the definition of “pixel”. It is somewhat redundant to name the subroutine “set pixel color” when we already know this is a subroutine for pixels. We are looking at definitions from the perspective of a pixel object.
Second, observe that we lost pix as a given and provide parameter. Again, this is because we are looking from the perspective of a pixel. As a result, the only statement of this subroutine is no longer refer to the color property as pix.c, the color property is merely c. This may look confusing because how do we know whose color property “c” this code is referring to?
To answer this question, let us move on and consider how we invoke “set pixel color” and “set color”. Let us assume that mypix is a pixel type variable. In the type-oriented approach, we set the color of mypix using the following code:
When mypix is of class pixel in the class-oriented approach, we color its color using the following code:
Hey, we use the dot notation to ”set color” just like we refer to a field in a type! You are right. This statement reads “invoke the set color method of mypix and pass the color red to parameter newcolor”. Because we are already saying “invoke the set color method of mypix”, it would have been redundant to specify mypix as a parameter to “set color”.
On the other hand, because “set color” must be invoked as a method of an “pixel” object, all references to the “pixel” object are implied for its fields.
This is why this point-of-view is called object-oriented, we are looking at fields and subroutines from the perspective of the object to which they belong!
One of the most useful features of object oriented program is the ability for a class to inherit from another class.
Inheritance has a lot analogies. For example, the class “ant” inherits from the class “insect”. From this inheritance, we know that all properties of “insect” exist in “ant” as well. If “insect” has six legs, we know automatically that “ant” also has six legs.
In the case of programming, we can say that “circle” inherits from “point” (or “pixel”). This means we automatically know that the “circle” class has properties like coordinate, color and transparency. In other words, we need not specify anything that is inherited more than once.
Of course, in addition of inheriting properties from the “pixel” class, the “circle” class also extends the “pixel” class by adding an additional property of radius. Note that extensions are not limited to properties (radius). A class inheriting from another class can also add more methods (subroutines). For example, the “circle” class has the additional methods “setRadius” and “getRadius”.
In an inheritance relationship, the class that inherits from another class is called a subclass, while the class inherited from is called a superclass.
In most object oriented programming languages, a subclass can change the definition of methods of its superclass. For example, the “draw” method of the class “pixel” only draws one pixel on the screen, but the “draw” method of the class “circle” may use the “draw” method of the “pixel” class, but it has to draw a complete circle.
In our pseudocode, we can use the following notation to indicate inheritance:
In object oriented, an abstract class is exactly what the name implies, a class that is abstract! Using our example, an abstract class is the class “shape” that represents the most abstract form of items that can be drawn on a computer screen.
What exactly is the “shape” class? Well, it looks like the following:
Okay, this resembles the definition of the “pixel” class, but note the lack of the method draw. All we say here is that there is a method called “draw”, but we don’t know how to do it. How can we specify how to draw when we don’t even know exactly what shape we are dealing with?
With this definition of class “shape”, we can refine our class “pixel” as follows:
Because a pixel is a particular shape, we can define the draw method for the class “pixel”. However, the class “pixel” is now much simpler because all the properties and methods that it shares with all other shapes are now moved to the definition of the class “shape”.
In short, an abstract class is a class that has at least one method declared and not defined. Note that an abstract class can be a subclass of another class. However, no variable (or object) can be instantiated by an abstract class (parameters are not objects, see the next section).
An abstract class forces its subclasses to supply the actual definitions of method declared “abstract” before objects can be instantiated. One significance of an abstract class is that it defines a template or mold for its subclasses. This is important for organization purposes.
Another significance of an abstract class, however, is that it provides the interface that is suitable for polymorphism. Polymorphism is the ability to change class “on the fly”.
Recall the circular queue that we defined before? Let us review its definition:
record circular queue
a : array of 8 slot
head : integer
count : integer
end record
Instead of using the “slot” type, let us use our new class “shape”:
record circular queue
a : array of 8 shape
head : integer
count : integer
end record
It may seem strange to use “shape” as the type of each slot in our circular queue. Afterall, “shape” is an abstract class and it does not even know how to draw! However, because “shape” is the abstract superclass of all other shapes, we can do the following:
Yes, we are “mixing up” the class “shape” and its subclasses “pixel”, “circle” and “rectangle”. This is okay because whatever you can do to “shape”, you can do to its subclasses as well. However, the following code is even more interesting:
Although the “remove from circular queue head” appears to remove an item of class “shape” from the queue q, it is, in fact, removing an item of some subclass of “shape”. In other words, although we claim that s is of class “shape”, it can actually be an object of any subclass of “shape”.
This is why we can invoke the “draw” method of s. If the algorithm removes an object of class “pixel” from q, the pixel is drawn. If the algorithm removes an object of class “circle” from q, the circle is drawn. Our algorithm does not care exactly to which subclass of “shape” the removed item belongs to. All the algorithm cares is that it wants to draw the item, however the draw method is implemented by the subclass.
To illustrate the concepts, let us take a look at some algorithms that we have already discussed. For example, let us consider the algorithm that finds the largest element in an array.
Although the initialization code takes time, the majority of time is consumed by the loop. As a result, we can often ignore the amount of time taken by the initialization. Besides, the amount of time to initialize does not depend on the size of the array (n), making it not important in the analysis.
Given there are n elements, there will be n- 1 iterations, while the condition i < n will be evaluated n times. One may be tempted to be very accurate and describe the number of times we need to perform the i < n comparison, the number of times we need to perform the m < ai comparison, the number of times we need to perform the m ← ai assignment and etc.
For most computer scientists, as n becomes a large number, missing one time is insignificant. This means it is safe to say there are just n comparisons and n iterations. Furthermore, we can make a worst case assumption that we need to perform the m ← ai operation for each iteration. This means there is, for estimation purposes, n m ← ai operations.
Since all operations are done approximately n times, we say the complexity of this algorithm is proportional to n.
Now, let us consider selection sort:
For this algorithm, the inner loop executes n - p - 1 times (where p goes from 0 to n - 1), while the outer loop
executes n - 1 times. As n becomes a large number, it is the operations in the inner loop that matters because they
are executed 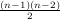 times, as opposed to the operations of the outer loop, where are only executed n - 1
times.
times, as opposed to the operations of the outer loop, where are only executed n - 1
times.
As a result, for large values of n, we can approximate the amount of time to execute the algorithm as 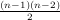 . As
mentioned earlier, computer scientists are not concerned with small margins. As a result, we look at
. As
mentioned earlier, computer scientists are not concerned with small margins. As a result, we look at 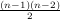 , which is
, which is
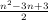 , and conclude that it is just proportional to n2.
, and conclude that it is just proportional to n2.
As a conclusion, the execution time of the selection sort algorithm is proportional to n2, where n is the size of the array to be sorted.
In its abstract form, O(f(n)) means the execution time of an algorithm approaches k × f(n) for some constant k and some function f as the size of the problem n approaches infinity (i.e., gets very large).
Practically speaking, an algorithm that has a complexity of O(n2) simply means the amount of execution time for a problem size n is proportional to n2. This means the amount of execution time for n = 2m is going to be about four times the execution time for n = m.
For example, using selection sort, if we time a computer and know that it takes 20 milliseconds to sort an array of 200 items, we know that it will take aabout 80 milliseconds to sort an array of 400 items.
The big-o notation is not supposed to give you an exact estimate of execution time. Instead, it indicates how the execution time scales with size of the problem. For most practical purposes, this is sufficient for comparing two algorithms.
For example, the merge sort algorithm has a complexity of O(nlog(n)), while the selection sort algorithm has a complexity of O(n2). It is true that the merge sort algorithm is useful mostly for sorting files and not arrays, and file operations are very slow compared to array (memory) operations. However, we can illustrate why this is not even an issue.
Let us assume that the constant for merge sort is 10 milliseconds (0.01 second), while the constant for selection sort is 10 microseconds (0.00001 second). In order to sort 10 records, merge sort takes 230 milliseconds, while selection sort takes 1000 microseconds or 1 millisecond.
It seems that merge sort is pointless.
Now, let us consider sorting 100 records. Merge sort takes 4.6 seconds, while selection sort takes 100,000 microseconds or 0.1 seconds. Still, there is no comparison.
Next, let us consider sorting 1000 records. Merge sort takes 69 seconds, while selection sort takes 10 seconds. Ah, the gap is closing.
When the problem size becomes 10,000 records, merge sort takes 921 seconds, while selection sort takes 1000 seconds. Merge sort has now taken over selection sort. Sorting 10,000 records may sound like a unrealistic task, but databases typically need to maintain millions of of records. Let us just bump up our problem size one more time to illustrate the concept of complexity.
Let us now consider 100,000 records. Merge sort takes 11,513 seconds, selection sort takes 100,000 seconds.
As the problem size continues to increase, the constants (0.01 seconds for merge sort and 0.00001 seconds for selection sort) play a very minor role for comparing algorithms. All the constants are doing is to determine the break even point of the two algorithms.
For this part of the project, you need to organize some classes and specify which one is a superclass of which other one.
This section describes the classes without any organization. As a result, many attributes are duplicated. The ordering here does not imply anything about the hierarchical organization.
Your job is to analyze these individual classes, and see how you can structure them to make it more organized. After restructuring, the class definitions must follow these rules:
In order to make the classes following these rules, you need to do the following:
Class definitions after your modifications. It must be typed, but you can use a regular text editor for this purpose.
This part of the project makes you think about the complexity of algorithms. Instead of performing mathematical analyses, we will just do some counting based on concrete test cases.
Part 1.
Refer to the binary search algorithm. Assume you have an array a of 10 items. The values (from a[0] to a[9]) are as follows: -200, -150, 0, 20, 21, 21, 50, 100, 100, 200 and 1000. Search for the value 19.
Count and let me know how many times each line of code is executed. Also add up all the execution count of every line and give me the sum. Do not count lines that end a construct, for example, “end while”. The same applies to “repeat”.
Part 2.
Next, do the same, but this time assume the array has 5 items, and this new array is simply the first half of the array we used previously. This time, look for the value -1.
Part 1.
Refer to the selection sort algorithm (see subsection 8.4.1). Assume you have an array a of 5 elements, and the values from a[0] to a[4] are as follows: 200, 3, 10, 5, 5.
Count and let me know how many times each line of code is executed. Also add up a grand total of the execution count of all the lines.
Part 2.
Next, do the same, but this time assume the array only has 4 elements, and their values (from a[0] to a[3]) are as follows: 4, 5, 2, 3.
Make a table out of each algorithm. Next to a statement, write down the execution count for each test case (part 1 and part 2). At the bottom of each algorithm, compute and write down the total execution count of all the statements.
It is probably best to use a spreadsheet (Microsoft Excel or OpenOffice Calc) for this one. However, a text file can also be used as long as the columns are aligned.
This assignment carries 400 points (twice as much as the previous ones). The due date is the last day of instruction, 2004/12/08. However, you may turn it in any time before year 2005. There will be no late deduction after the due date. The early points (2% per day) still applies.
I suggest that you try to do this as soon as possible, because this assignment will help you prepare for the final exam on 2004/12/13.
Turn this assignment in as one or multiple files and email to tauyeung@drtak.org. The subject of the message must say
cisp300 project3 by your name
|
Replace your name with your actual name. Submissions not following this rule will be deducted 50 points!
Although the price of memory drops very quickly, they cannot match the drop of hard drive (mass storeage) space. A modern computer has about 512MB (mega bytes) of memory, while it probably has 80GB (giga bytes) of mass store. The mass store of a “typical” computer is about 160 times the size of memory.
This means we can create files to store information that are far larger than the size of memory. This is especially true for operating systems that has no software limitation of file size. Microsoft Windows, even XP, has a limitation of 2GB per file. This limitation does not exist in, for example, Linux, FreeBSD and MacOS X (which is based on FreeBSD).
This chapter discusses what a “file” really means from the perspective of computer programming. We will also discuss a useful algorithm for files called merge sort.
Most people who use computers understand what an ordinary file is. When you use a word processor and decide to save the document, it is saved to a file. Once saved to a file, you can later turn off the computer and expect the file to persist. After you power up the computer later, you can load the file into the word processor and continue your work.
A file of this sort is basically an entity on a mass store device (such as a hard disk, a flash drive, a floppy disk (in a drive) and etc.). Although this type of files account for most files in a computer environment, they are not the only files a computer needs to handle.
For convenience, many devices in a computer are also considered files from an application program’s perspective. What are devices? Devices is a term that applies to components of a computer that serves a particular purpose. For example, the parallel port can be considered a device. Each serial port can be considered a device. The output of a sound card can be considered a device.
None of these devices, however, actually “store” any information. That is correct. Nonetheless, the inability to store is not a requirement of a file in a computer environment.
A file is an illusion produced by an operating system. Without an operating system, a hard drive contains sectors, tracks and drums of little magnets aligned one way or another. Without an operating system, a flash drive contains specialized transistors that can hold a small charge even when powered off. Without an operating system, a serial port is a component that serialize data and send a bit stream out (or receive a bit stream) at a predetermined rate.
An operating system “unifies” the interfaces to all of these different devices. Instead of bombarding a programming with many subroutine, one to initialize a serial port, one to initialize a file in an HD, one to initialize a file on a floppy disk and etc., there is only one interface to “open a file”. Instead of having one interface to read a byte from the serial port, one interface to read a byte from the mic-in from a sound card, one interface to read a byte from a ZIP disk, there is one interface to “read a byte from a file”. Because there is only one interface to perform an abstract operation, a programmer only needs to learn a small set of interfaces.
Note that this concept relates to ADT. A file is really an ADT because an operating system is hiding many different ways of handling difference devices in the back. However, to an application programming, the interface to all files is the same. In the next section, we look into the types of operations one can perform to a file.
There are four basic file operations. This section only discusses these four basic ones. In an actual programming language class, you may learn additional operations for files.
The “opening” of a file is the first access to a file. An “open” operation translates to a request to the operating system. An application program needs to tell the operating system which file to access (using the name of the file) and how to access (read or write). The operating system then checks to make sure the request is reasonable, and returns a record that represents the interface to a file.
For pseudocoding purposes, we use the following code to open a file:
Note that “file” in this code is merely the name of a class that is used to represent a file in memory, and f is a variable of this type. “open” is a method provided by class file to request access to a particular file. “write_access” is an integer constant that specifies that we are requesting to write to the file. Parameter result is true if and noly if the request is granted.
The “closing” of a file tells an operating system that an application program is done with a file. The operating system, as the coordinator, can then grant other programs access to the same file. Depending on the nature of the device behind the file representation, various clean up operations are performed when a file is closed.
A close operation tells the operating system that we are done using a file:
A read operation tells the operating system to read something from a particular file (represented by a variable of “file” type). The read operation is implemented slightly differently for different languages. For pseudocoding purposes, we’ll use the following convention.
For example, to read an integer from a file represented by f into an integer variable i, one can use the following statement:
A write operation tells the operating system to write something to a particular file (represnted by a variable of “file” type).
For example, to write an integer value i + 5 to a file represented by f, we can use the following code:
In most operating systems, a file is merely a “stream of bytes”. A byte is 8 bits (a bit is a binary digit). How do we go from chunks of 8 bits to the kind of information we can read from/write to a file?
For example, in a spreadsheet file, we can store all kinds of information. We can store names, addresses, as well as formula, numbers and even graphs. Is everything represented by chunks of eight bits?
The answer is yes! In fact, even picture, sound, and movie files are no more than sequences of bytes. Really!
In order to view a photograph that is encoded as a GIF file, you need to use a viewer that knows how to interpret contents of a GIF file. Similarly, to play music from an MP3 file, you need a program that knows how to interpret contents of an MP3 file. In other words, to make use of the information contained in a file, you need to use the approprate program to interpret it. Similarly, you also need appropriate programs to encode information into various file formats.
The interpretation of GIF, MP3 and other file formats is out of the scope of this class. However, we do want to at least touch on some basic mechanisms to interpret bytes from any file.
This is a common method to store numeric values in a file. A binary number has a fixed width (number of bits), and it is used to represent numeric values in base 2. Let us assume that we want to represent both positive and negative values in this section.
Using 8 bits (one byte), we can represent values from -128 to 127. The value 67, for example, has a binary representation of 010000112. In other words, when a program encounters a byte of bit pattern 010000112, it has the option to interpret it as an 8-bit signed number with a value of 67.
Using 16 bits (two bytes), we can represent values from -32768 to 32767. For example, the value 5000 has a binary representation of 00010011100010002. Here, we have a little problem. Since the smallest chunk size of a file is a byte (8 bits), we need to somehow chip a 16-bit number into two bytes. The chopping part is easy, we call the most significant 8 bits the most significant byte (bit patter 000100112 in our example), and we call the least significant 8 bits the least significant byte (bit pattern 100010002 in our example).
Which one should be the first byte, and which one should be second? All bytes within a file are ordered, including the two bytes required to store a 16-bit signed number.
There are two standards. The “Little Endian” approach stores the least significant byte first. In our example, the 16-bit representation of 5000 is stored as 100010002, then 000100112. This standard is used mostly by PCs.
The other standard, called “Big Endian”, stores the most significant byte first. In our example, the 16-bit representation of 5000 is stored as 000100112, then 100010002. This standard is used mostly by Macs and TCP/IP (networking standard).
Note that the little endian and big endian methods apply to wider binary numbers.
We now have a method to represent numbers as bytes in a file. How about information that is not numeric, such as names?
To store text information, each individual unit is a character. While this is easy for alphabet-based languages (English and most European languages), it is not as easy for pictogram-based languages (such as Chinese).
In the early days of computing and telecommunication, English was the dominant language. As a result, there is ASCII (American Standard Code for Information Interchange) as a standard. EBCDIC (Extended Binary Coded Decimal Interchange Code) is another standard used in the early days, but it had been obsoleted for a while now.
Using the ASCII standard, each typewriter symbol is encoded by an 8-bit bit sequence. Lower case ‘a’, for example, is encoded by the bit pattern 011000012. As a result, one character is one byte. To spell out the name “John”, the bit sequence becomes 010010102 (J), 011011112 (o), 011010002 (h), 011011102 (n).
As computers become internationalized, it became important to also be able to represent alphabets and characters of other languages. Through many years of evolution, Unicode was finally developed as an encoding scheme that accommodates “all” languages, including Klingon.
With 8 bits, we can only represent 256 distinct characters. Obviously, there are more than 256 distinct symbols when we sum up all the alphabets and character sets of the world. As a result, Unicode uses two bytes (16 bits) to represent one character. This means each character is a symbol selected from a total of 65536 possible selections. Even to date, Unicode still has “room” for more languages!
Since each Unicode requires two bytes, it is important to know whether a file uses Little Endian or Big Endian representation. Unfortunately, Unicode does not specify the endian-ness (endianity, endity?).
Is it upper case ‘O’, or is it an 8-bit binary number representing the value of 79?
It depends on the program that interprets the file. A byte in a file has no meaning until a program reads it and use it to perform some operations. For example, if 010011112 is read from a file and displayed directly on a screen, it is being interpreted as an ASCII character.
However, if 010011112 is read from a file, and it is multiplied by another number, it is being interpreted as an 8-bit integer.
Besides the ASCII character ‘O’ and the 8-bit integer value 79, the bit pattern 010011112 has an infinite number of interpretations. For example, it can be the most significant byte of a 16-bit integer,
In actual programming, you need to use a programming language (sometimes a few) and the associated tools. A programming language is the syntax and meaning of statement, definitions and etc. In the real world, you are likely to use programming languages such as C, C++, Java, Visual Basic, Cobol, Fortran, Perl, PHP and etc. Most languages offer constructs similar to the pseudocode syntax that we have been using in this course.
A program written in a programming language cannot be understood by a computer. Natively, a computer (or the processor of a computer) only understand instructions specified as bit patterns. Such instructions are often very primitive and do not resemble constructs that we discuss in this class.
As a result, a programming written in a high level programming language, such as C, C++ and etc., must be translated to the level where the processor can understand. There are mainly two method to translate a program so a processor understands.
The first method is called compilation. A compiler is like a book translator who reads your program written in a high level programming language. It checks your program against syntactic (grammar) rules as well as some semantic (meaning) rules. If all checks out, a compiler also output assembly code or machine code that a processor understands. A particular source code file only needs to be compiled once because the generated assembly code or machine code is stored in other files. Langauges that fall into this category include some implementations of Pascal, almost all implementations of C and C++ as well as Fortran.
The main advantage of a compiled language is execution speed. A compiler can optimize the output code to gain execution speed at the expense of compilation time. Another major advantage of compilation is that the compiler can catch syntax errors as well as bad usage early. A programmer does not need to run a program to locate and eliminate certain types of bugs. A drawback of a compiled language is that for large and huge programs, the amount of time to recompile a program can be quite lengthy.
Note that most compiled languages are “strongly typed”. This means type checking is only enforced, but enforced to the extreme. In systems programming and some application programming, this is a very desirable feature. Such languages also tend to require that variables be declared before a program can use them. Again, this is a useful feature.
The second method is called interpretation. An interpreter is like a live interpreter in major international conferences. It reads a small chunk of a program written in a high level language, then immediately translates it to actions that a processor can perform. The processor performs the actions and forget the translated actions. The interpreter then reads some more and repeat this process. Languages that fall into this category are mostly “scripting” languages such as Javascript, shell, batch files, Perl and PHP.
Huge programs written in an interpreted language do not require any compilation time to prepare the programs for running. This is an advantage, especially for RAD (rapid application development). Most interpreted languages have extremely flexible type/variable binding. In other words, the type of a variable can morph as a program executes. This is both an advantage and a disadvantage. It is an advantage for symbolic processing programs because the same symbol can be interpreted differently depending on the context. This is a disadvantage for systems software because rigid type checking can identify potential programs in systems software.
Interpreted languages also allow on-the-run modification. This means a program can be running while portions of it (modules) are updated. It is not necessary to shut down an application to update/debug/enhance it. This feature is particularly useful for applications where modules are “loosely connected”. For example, in CGI applications, pieces of a web application often execute with limited interdependency.
However, because an interpreter only interprets (parse and analyze) chunks of a program on demand, even syntactic errors go unnoticed until a program executes to the parts with syntactic errors. Needless to mention, wrong or questional usage do not get detected until those portions of a program get executed. The end result is a more lengthy debugging process because most bugs cannot be detected until the program is executed.
Some languages, such as Java and Visual Basic (.NET), use a combination of compilation and interpretation. In Java, for example, high level source code is first compiled to “byte code”. “Byte code” are low-level instructions that are not native to a particular processor. A virtual machine then executes these byte code in an interpretation fashion. In other words, a virtual machine is a piece of software that reads chunks of byte code, translates them to native operations, and repeat the process.
Compiled-interpretive languages have certain advantages. For example, Java has the advantage of being able to identify bad syntactic constructs and questionable semantics during the compilation phase. At the same time, the compilation time is not as lengthy as a compiled language like C and C++. Compiled-interpretive languages offer the same on-the-run modification flexibility as interpreted languages.
The main disadvantage of a compiled-interpretive language is execution time. Programs written in such a language always execute slower than their equivalent written in a compiled language. Even the equivalents written in an interpreted language execute at about the same speed.
For a real programming language, however, its syntax becomes much more important. This is because when a computer attempts to understand a program, it has to strictly follow very specific rules. This makes sure there is no ambiguity, and also that bad constructs are identified as early as possible. Another side benefit is that a computer understands programs written following strict and specific rules very efficiently.
BNF (Backus-Naur form) is a well established syntax for, guess what, specifying syntax! Although BNF is widely used to specify programming languages in the context of compilers, it is a little cumbersome and difficult to use for describing the syntax of a programming language to most people.
As a result, EBNF (Extended BNF) was invented to describe syntax more effectively. Note that any syntax that can be described by EBNF can be described by BNF, and vice versa. EBNF is “extended” to make descriptions more concise, and easier to understand for people.
An excellent article is http://www.garshol.priv.no/download/text/bnf.html. It has a very in-depth treatment of this subject matter.
These are just fancy names for “to-be-determined” and “determined”. A token is a symbol that should be replaced by something else. A grounded symbol is a symbol that specifies literally what should be in a program.
Tokens are usually specified as phrases enclosed in angle-brackets (<>). Sometimes the angle-brackets are omitted to make productions more concise. For example, <name> is a token. Note that BNF and EBNF are not related to HTML or any markup language. Therefore, <name is not the beginning of a tag!
Grounded symbols are often specified as double-quoted text. For example, "Tak" is a grounded symbol. Note that the pattern appearing in double-quotes should appear verbatim (with no alteration) in a program.
A production is a fancy name for “expansion rule”. In other words, a particular production specifies how a token can be expanded. Note that a token can expand to other tokens. In a production, the left hand side specifies one and only one token to be expanded. The right hand side specifies a sequence of tokens and/or grounded symbols that takes the place of the expanded token. Two adjacent components of a sequence are separated by spaces in some representation. However, some presentations use a comma (,) to separate two adjacent components. The two sides of a production are separated by colon-colon-equal (::=).
To specify a name, for example, we can use the following production:
<name> ::= <first-name> " " <last-name>
|
Note that <first-name> and <last-name> still need to be expanded. However, the space between them is grounded. This rule essentially says “a name is a first name, followed by a space, then a last name”.
A token can have multiple productions. For example, in France, there is a list from which citizens can choose first names from. This can be represented by a bunch of productions as follows:
<first-name> ::= "Sean"
<first-name> ::= "Pierre" <first-name> ::= "Luc" |
If a token has multiple productions, that means it can use any one of the productions. In other words, the productions are alternatives. In our previous example, the rules specify that a first name can be Sean, Pierre or Luc.
BNF ends here. With only these simple rules, BNF can be used to describe any context-free language. All programming languages are context free. However, although BNF is expressive enough, it is generally considered difficult for people to understand. This is why we have EBNF.
EBNF allows grouping. A “group” is a sequence of tokens and grounded symbols in curly braces ({}). For example, {<first-name> " " <last-name>} is a group.
A group is not useful by itself. However, grouping is very important when we use other features of EBNF.
EBNF allows the specification of optional parts of productions. Optional components are enclosed in square brackets ([]). For example, we can add <title> as an optional part of a name. This can be done as follows:
<name> ::= [<title> " "] <first-name> " " <last-name>
|
Another method to specify optional is to use the suffix ? after an optional token, grounded symbol or group. This notation is less commonly used. In our example, the production can be specified as follows:
<name> ::= {<title> " "}? <first-name> " " <last-name>
|
Note that you can include a sequence as the optional part of a production.
EBNF makes is possible to specify alternatives in a single production. For example, we can say that a name can be first-name-first, or last-name-first (with a comma). To specify the alternatives, we use the vertical bar (|) to separate alternative sequences. In our example, we rewrite the production as follows:
<name> ::= <first-name> " " <last-name> | <last-name> ", " <first-name>
|
While this is not too ambiguous, it is always better to make sure everything is absolutely clear. We can use curly braces (grouping) to make sure that the reader understand the syntax. The following production is more clear with curly braces:
<name> ::= {<first-name> " " <last-name>} | {<last-name> ", " <first-name>}
|
The addition of grouping makes sure a reader understand the entire sequence <first-name> " " <last-name> is an alternative to the entire sequence <last-name> ", " <first-name>.
You can specify that a token, grounded symbol or group can repeat. This is accomplished by appending the symbols * or + after a token, grounded symbol or group. + means “at least one of the previous thing”, while * means “any number of the previous thing”.
Let us assume that <lcase-char> expands to one of the 26 lower-case English letters, and ucase-char> expands to one of the 26 upper-case English letters. We can, then, specify a general-name as follows:
<general-name> ::= <ucase-char> <lcase-char>+
|
This means John, Mary and etc. are all valid general names. However, single letter names, such as T (as in Mr. T), J (as in J in MIB) and K (as in K in MIB) are not permitted.
If you want to permit single letter names, then you have to say that a name can have any number (including zero) of lower case letters:
<general-name> ::= <ucase-char> <lcase-char>*
|
The difference is subtle, but nonetheless very important.
Also note that the space between ucase-char> and lcase-char is not a part of a name!
You can also specify that a token, grounded symbol or group must repeat a ranged number of times. This is done by superscript and subscript. The superscript specifies the upper limit, while the subscript specifies the lower-limit.
This notation is very rarely used.