A loop is a control structure that permits certain steps in a program to be repeated. Without loops, programs cannot perform certain steps again and again, often without knowing exactly the number of times to repeat.
In real life, we often rely on loops as well. For example, the logic of eating is iterative. Let’s think about eating a relatively large order of food. The basic step is “eat a spoonful” (or whatever quantum of food you want to use). Ahead of time, we don’t know exactly how many spoonfuls is necessary. The proper logic to eat a meal is “eat as many spoonfuls as possible until you feel full”.
Let us explore loops, again. However, this time, we use a special kind of structure. Let us take a look at the algorithm to eat in algorithm 1.
Now, let’s take a closer look at this block of code.
No explanation is complete without a trace. Table 1 illustrates the steps taken when someone only needs three bites to become full.
| line # | comment |
| 1 | this is not necessary since it doesn’t do anything |
| 2 | this is the first bite |
| 3 | the condition is evaluated, one is not full, yet |
| 1 | this part is important, we get back to this line because the condition is not true |
| 2 | this is the second bite |
| 3 | the condition is still false |
| 1 | since one is not full yet, here we go again |
| 2 | this is the third bite |
| 3 | this time around, one is full, and this condition is true now; we don’t have to take another bite! |
| 4 | once a loop exits, a program continues with the line following the “until” marker. |
There is a problem with algorithm 1. What if someone is already full? A special property of a “repeat” loop is that the action is performed at least once. This is because the “until” condition is evaluated after the action is performed.
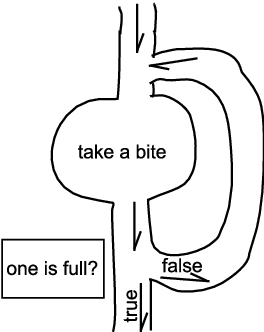
Let’s look at a “trail map” of algorithm 1 in figure 1.
In a trail map representation, each path is one-way only. The top junction is a merge junction, which means the top and right paths merge into the down path. The bottom junction is a fork, which means the top path splits into the down path and the right path. The rectangle labeled “one is full?” is the question to answer. Depending on whether the answer is “true” or “false”, the bottom or right path is chosen, respectively.
Since we concluded that algorithm 1 is not perfect, there must be a better way. What we need is a loop construct that evaluates the condition first to see if an iteration is necessary, then perform the action only if it is necessary.
This loop structure is as displayed in algorithm 2.
This control structure looks like a “repeat” loop reversed. Let’s explain each line in algorithm 2.
Table 2 is a trace of algorithm 2.
| line # | comment |
| 1 | because the person is full already, the condition “one is not full” is false |
| 4 | when the condition of a “while” loop is false, the loop is terminated. Execution moves to the line immediately following the end marker. |
No explanation is complete without a picture. Figure 2 illustrates the logic of algorithm 2. You can tell that it is a loop because of the loop-back branch on the left hand side. Note that this loop back goes from bottom to top. Also note the branching fork is below (or after) the merge point. This means that when we loop back after taking a bite, we always reevaluate the condition “one is not full”, then determine whether to take the “true” path or “false” path.
Some languages support the concept of “repeat”, but C and its derived languages do not have repeat. Instead, such languages have an “upside down while”. Let us illustrate with an example.
Let us consider algorithm 3 as an example.
This logic keeps asking for a ZIP code until a valid one is entered. Note that because this is a repeat-until loop, the action (asking for a ZIP code) is performed before asking the question whether the ZIP code is valid. This only makes sense.
In C (and its derived languages), this logic is expressed as follows:
It doesn’t seem very different. Instead of “repeat”, we use “while”, and we use “while” to end the construct instead of “until”. However, a closer look reveals a major difference. In the repeat version, the condition is “the ZIP code is valid”. However, in the do-while version, the condition is “the ZIP code is not valid”.
In other words, a repeat-until loop specifies an exit condition (when true, exit). A do-while loop, however, specifies a do-it-again condition (when true, do it again).