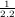of a kg at one gravity pull. Reversing this relationship, one kg is 2.2 pound (mass). From now on, we
should use kg for mass.
The first property of a vehicle is its mass. The SI (Internation Standard, but in French) unit is kg (kilogram). In the U.S., mass is measured by “pound”. Pound is really a measuring unit for force (we’ll get to it). The relationship between kg and pound (for mass) is as follows:
One pound (force) is 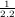of a kg at one gravity pull. Reversing this relationship, one kg is 2.2 pound (mass). From now on, we
should use kg for mass.
It’s not that hard. A 1996 Miata is about 2200 pounds, that converts to about 1000kg.
The physics symbol for mass is “m”.
Distance is, well, distance. The U.S. unit is a foot. The SI unit is a meter. A meter is about 3.28 feet. That is pretty simple. The physics symbol for distance is “D”.
Speed is the amount of distance traveled in a certain amount of time. The U.S. unit is mph (miles per hour), the SI unit is km/h (kilometer per hour). One mile is about 1.6 km. In science, however, it is more common to measure speed by meter per second, or ms-1.
The physics symbol for speed (velocity) is “v”.
Acceleration is the change of speed over time. For example, it determines how long it takes to accelerate from 0mph to 60mph. Let’s say a sports car accelerates from 0mph to 60mph in 6 seconds. This is how we compute the acceleration.
The physics symbol for acceleration is “a”.
One mile is 1.6km, so 60mph is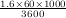 
ms-1 = 26.67ms-1. The change of speed is, of course, 26.67ms-1, over 6 seconds.
The acceleration is, then, 
= 4.445ms-2.
Force is the acceleration of mass. Naturally, the SI unit of force is kg × m × s-2. This mess is also called a Newton (N).
Getting back to our example, let’s consider a Miata accelerating from 0mph to 60mph in 6 seconds. The mass of a Miata is 1000kg. This means to accelerate a Miata from 0mph to 60mph in 6 seconds, we need 4445N.
The physics symbol of force is “F”.
A wheel does not exert force directly. A wheel exerts torque. Torque is closely related to force. Torque is force applied at a distance from the center of rotation. The SI unit of torque is Nm.
In our example, the diameter of a 185/60R14 wheel/tire combo is 596mm. The radius is 298mm. The amount of torque is 4445N × 0.298m = 1325Nm. Because there are two wheels applying torque at the same time, each wheel only needs to exert 663Nm.
The U.S. unit to measure torque is pound-foot. Let see how we can do the unit conversion. A kg at one gravity pull is 2.2 pounds (force). One gravity is 9.8ms-2. This means one kg at one gravity pull is 9.8N. Since 9.8N is 2.2 pounds, the conversion is that one pound is 4.45N. One foot is 0.3m. This means that one pound-foot is 1.35Nm. The required torque in our example is, then, 491 pound-foot at each wheel.
The physics symbol of torque is “τ” (tau).
Energy is force applied over distance. In our example, let’s first figure out how far the Miata needs to accelerate to 60mph.
D = vt, where D is distance, v is velocity and t is time. While accelerating, D =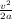 
, where v is the ending velocity. This
means D in this case is 80m.
Work done is force (4445N) times distance (80m), so the energy used to accelerate the car is 355600Nm. One Nm is also called a Joule (J). The engine must be able to output 355.6kJ. Since this much energy is converted in 6 seconds, the engine has an output of 59.27kW. This converts to about 79.48 horse power.
The previous section assumes acceleration is constant. That, unfortunately, is not true. Given the same amount of power,
acceleration decreases as velocity increases! We can understand this from the point of view of kinetic energy. Kinetic energy is
E =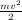 
. You can see that E increases quicker than v because of the square function. This also means that
an object gains kinetic energy faster than it gains speed. An object has 4 times the energy when its velocity is
doubled.
How about the torque specification? We figured that we need 491 pound-foot at each wheel. However, this is based on the assumption of constant acceleration. Furthermore, car specification usually measures torque at the crank shaft. As if things are not sufficiently complex, there is the transmission and differential between engine shaft and wheels.
Let us think for a moment. The specification mentions 114 pound-foot at 5500rpm. This translates to 153.9Nm. In first gear, the transmission has a ratio of 3.136:1. The differential has an additional 4.1:1 reduction. Combined, there is a 12.86:1 reduction. Torque increases proportionally as gear ratio increases. As a result, in first gear, at 5500rpm, there is a total of 1979Nm at the wheels. This translates to 6754N. At that instant, the acceleration is 6.754ms-2.
Frictional force is a proportion of the force applied perpendicular to the surface where two materials meet. Friction coefficient varies depending on the materials that are in contact.
Static friction applies when two objects are not sliding relative to each other, and the cofficient is usually denoted as μs. Kinetic friction applies when two objects slides, and its symbol is usually μk. For street tires, μs = 0.7 for dry paved road and μs = 0.4 for wet paved road. Note that μk for wet paved road can be very low, which means locking the tires in the rain can be very dangerous!
Friction is used for many purposes. Acceleration, braking, turning all rely on friction. Consequently, friction is an important factor not only for performance driving, but also safe driving.
The center of mass of a vehicle is the one point at which you can imagine the entire mass of the vehicle is. When a vehicle is stationary, the center of mass is also the center of gravity. However, when a vehicle is accelerating, decelerating or cornering, the center of gravity “shifts”.
The gravitational force of a vehicle points directly to the center of the earth. An additional force, such as acceleration or braking, can change the total vector of force acting on the vehicle.
For example, in our example, a Miata can achieve an acceleration of 6.75ms-2 horizontally. When this is combined with the gravity of 9.8ms-2 vertically, the total force acting on a Miata is (6.752 + 9.82)-2 = 11.90, pointing at a direction that is about 55.44 degrees down to the rear.
This is pictorially represented here:
“L” is the length between the two axles. “g” is gravity, and “a” is acceleration. “z” is the distance between the axle height
and the center of mass. x =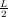 
+ z
, y = 
- z
.
Assuming the total weight of the vehicle is “w”, the weight on the front (left) axle is wf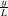 = w
, and the weight on the rear
(right) axle is wr = w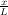
.
Note the proportion of weight shift depends not only on “a” (acceleration), but also “z”. A lower profile vehicle, therefore, experiences less weight shift.